Branch and Bound Algorithm is a technique used in computer science and optimization to solve problems by exploring all possible solutions. It is a strategy for finding the optimal solution to a problem, especially when the problem has a large number of possible solutions. The Branch and Bound Algorithm involves systematically exploring the space of possible solutions by branching off into subproblems and bounding the solution space by setting constraints on the possible solutions.
Branch and Bound Algorithm is commonly used in combinatorial optimization problems, such as the Traveling Salesman Problem and Knapsack Problem, where the goal is to find the best possible solution from a large number of possible solutions. It is a powerful technique for solving complex problems that would otherwise be computationally infeasible to solve.
How Branch and Bound Algorithms Work
- Generate an initial solution to the problem.
- Set the current best solution as the initial solution.
Step 2: Branching
- Divide the solution space into smaller subproblems, or branches, by creating new subproblems based on the current problem.
- Choose a variable to branch on and create subproblems by assigning values to that variable.
- Create a subproblem for each possible value of the variable.
Step 3: Bounding
- Evaluate the subproblems using a bound function that estimates the minimum or maximum value of the solution for each subproblem.
- Prune, or eliminate, branches that have a minimum or maximum value estimate worse than the current best solution.
- Update the current best solution if a better solution is found.
Step 4: Repeat
- Continue branching and bounding until a solution is found or all possible solutions have been explored.
The Branch and Bound Algorithm can be used for both maximization and minimization problems. For maximization problems, the bound function estimates the maximum value of a solution for a given subproblem. For minimization problems, the bound function estimates the minimum value of a solution for a given subproblem.
Lets take an example of Traveling Salesman Problem (TSP), suppose a salesman needs to visit four cities: A, B, C, and D. The algorithm can generate an initial solution, such as visiting the cities in the order A, B, C, and D. The algorithm then branches off into subproblems, such as visiting the cities in the order A, C, B, and D, or A, B, D, and C.
The algorithm then uses a bound function to estimate the minimum distance that can be traveled for each subproblem, and prunes branches that have a minimum distance estimate greater than the current best solution. The algorithm continues to branch off into smaller subproblems until it finds the optimal solution or explores all possible solutions.
Here is the solution of a TSP with 7 cities using Branch and bound algorithm.
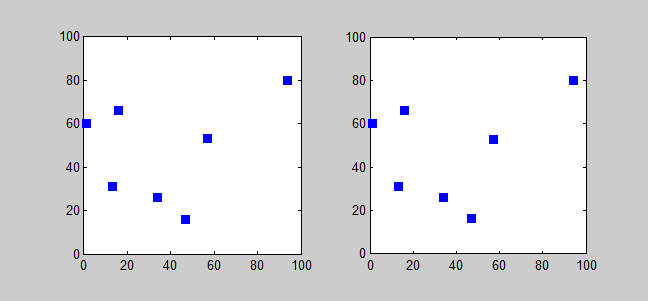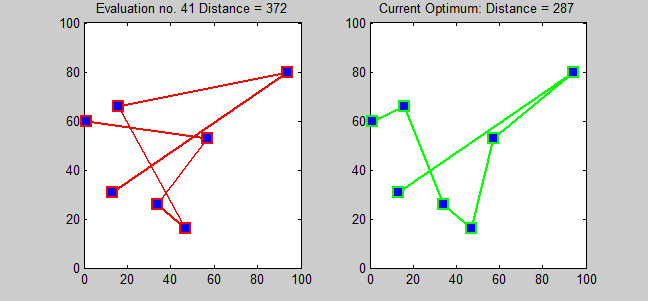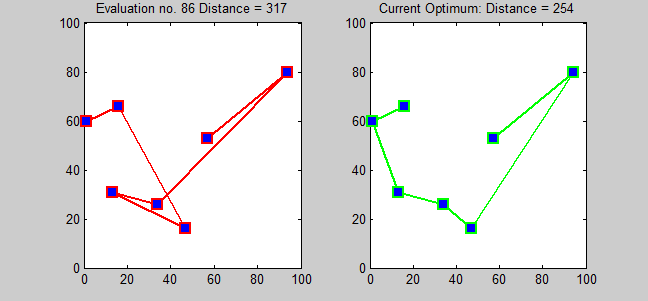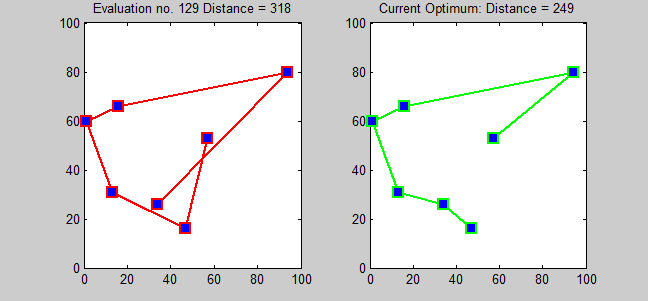
Advantages of Branch and Bound Algorithm
- Guaranteed optimality: Branch and bound algorithms guarantee that the optimal solution will be found, provided that certain conditions are met. This is because the algorithm systematically explores the entire search space and eliminates subspaces that cannot contain the optimal solution.
- Can handle large search spaces: Branch and bound algorithms are particularly useful when the search space is large, as they can explore the space in a more efficient manner than brute-force methods.
- Can handle nonlinear objective functions: Branch and bound algorithms can handle nonlinear objective functions and constraints, which makes them applicable to a wide range of optimization problems.
Disadvantages of Branch and Bound Algorithm
- Computationally intensive: Branch and bound algorithms can be computationally intensive, particularly for large search spaces or complex objective functions. The algorithm may require a significant amount of computational resources to explore the entire search space.
- Requires a good branching strategy: The efficiency of the algorithm depends heavily on the branching strategy used. A poor branching strategy can result in a suboptimal solution or even cause the algorithm to fail.
- May require manual tuning: The algorithm may require manual tuning of certain parameters, such as the branching factor or the pruning rule, in order to achieve good performance. This can be time-consuming and requires expert knowledge.
Difference Between Backtracking and Branch and Bound Algorithms
The main difference between backtracking and branch and bound algorithms lies in their approach to search space exploration and pruning. Backtracking explores the entire search space exhaustively and prunes partial solutions that violate constraints, while branch and bound partitions the search space into smaller subspaces and eliminates subspaces that cannot possibly contain the optimal solution. As a result, branch and bound algorithms are typically more efficient for large search spaces with complex constraints and objectives.
Standard problems for Branch and Bound Algorithm
- Traveling Salesman Problem: TSP seeks the shortest possible route that visits a set of cities exactly once and returns to the starting city. Branch and Bound is used to explore promising paths while pruning those that cannot lead to an optimal solution.
- Integer Linear Programming: In Integer Linear Programming, the objective is to find integer values for variables that optimize a linear objective function. Branch and Bound is employed to explore feasible solutions efficiently.
- 0/1 Knapsack Problem: In the 0/1 Knapsack Problem, items have weights and values, and the goal is to maximize the total value while respecting the knapsack's capacity. Branch and Bound efficiently explores feasible solutions.
- Graph Coloring: Graph Coloring involves assigning colors to vertices of a graph such that no two adjacent vertices have the same color. Branch and Bound is used to explore color assignments while minimizing the number of colors.
- Maximum Clique Problem: The Maximum Clique Problem involves finding the largest complete subgraph (clique) in a given graph. Branch and Bound helps explore potential cliques while eliminating unpromising candidates.
- Job Shop Scheduling: In this scheduling problem, jobs with different processing times are assigned to machines to minimize the total completion time. Branch and Bound helps explore different schedules systematically.
- Subset Sum Problem: This problem involves finding a subset of a given set of numbers whose sum matches a specified target. Branch and Bound helps explore subsets and eliminate branches that cannot lead to an optimal solution.
