
Heap Data Structure
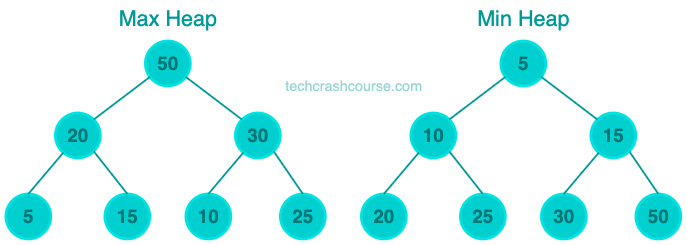
Heap data structure is a complete binary tree-based data structure. In the heap, the parent node is either greater than or less than the child nodes. If each node is greater than the child nodes, it is called a Max Heap, and if it is less than the child nodes, it is called a Min Heap.
The heap is a complete binary tree, meaning that all levels are completely filled except possibly the last level, which is filled from left to right. In a max-heap, Every node is greater than or equal to its children. In min-heap, Every node is less than or equal to its children.
Common Use Cases of Heaps
- Priority Queues : Heaps are often used to implement priority queues where elements with higher priority (max-heap) or lower priority (min-heap) are served before others.
- Heap Sort : Heap Sort is a sorting algorithm that uses a max-heap or min-heap to build a sorted array.
- Dijkstra's Algorithm : In graph algorithms, heaps are employed in Dijkstra's shortest path algorithm to efficiently select the vertex with the minimum distance
- Job Scheduling : Heaps can be used in job scheduling systems where tasks with higher priority need to be executed first.
- Memory Allocation : Operating systems use heaps for memory allocation and deallocation.
Advantages and Disadvantages of Heap Data Structure
Advantages of Heap
- Fast insertion and deletion of elements: The heap data structure provides fast insertion and deletion of elements. The insert and delete operations take O(log n) time complexity.
- Constant time access to the maximum/minimum element: The heap data structure provides constant time access to the maximum/minimum element.
- Efficient implementation of priority queue: The heap data structure is an efficient implementation of the priority queue.
Disadvantages of Heap
- Inefficient for searching: The heap data structure is not efficient for searching elements. The search operation takes O(n) time complexity.
- Not suitable for all types of operations: The heap data structure is not suitable for all types of operations. For example, if we need to find the median element of a set of data, then the heap data structure is not suitable.
- Large memory requirements: The heap data structure may require a large amount of memory to store the elements, especially for large data sets.
Heapify Operations in Heap
Heapify operation is an operation that maintains the heap property of the heap. The heapify operation is usually performed on a subtree of the heap to maintain the heap property. Heapify operation can be performed in two ways:
Bottom-up Heapify Operation
The bottom-up heapify operation is a simple process that is used to maintain the heap property of the heap. In this operation, we start from the last element of the heap and heapify the elements until the root of the heap.
Here is a step by step guide to perform bottom-up heapify
- Start from the last element of the heap.
- Check whether the parent node is smaller than the child node or not.
- If the parent node is smaller than the child node, then swap the parent node with the child node.
- Continue the above step until the root of the heap.
Top-down Heapify Operation
The top-down heapify operation is another process that is used to maintain the heap property of the heap. In this operation, we start from the root of the heap and heapify the elements until the bottom of the heap.
Here is a step by step guide to perform top-down heapify
- Start from the root of the heap.
- Check whether the parent node is greater than the child node or not.
- If the parent node is greater than the child node, then swap the parent node with the child node.
- Continue the above step until the bottom of the heap.
Common Heap Operations
Insert Operations in Heap
The insert operation is used to insert a new element into the heap. The new element is inserted at the end of the heap and then heapify operation is performed to maintain the heap property.
The following are the steps to perform the insert operation:
- Insert the new element at the end of the heap.
- Perform the bottom-up heapify operation.
Delete Operations in Heap
The delete operation is used to delete an element from the heap. The element is deleted from the root of the heap, and then heapify operation is performed to maintain the heap property.
The following are the steps to perform the delete operation:
- Delete the root element from the heap.
- Replace the root element with the last element of the heap.
- Perform the top-down heapify operation.
Extract Max/Min Operation in Heap
The extract max/min operation is used to extract the maximum/minimum element from Max/Min heap respectively.
The following are the steps to perform the extract max/min operation:
- Extract the root element from the heap.
- Replace the root element with the last element of the heap.
- Perform the top-down heapify operation.
Heap Data Structure Implementation Program
In this tutorial, we will explore the array implementation of the heap data structure. Heaps are commonly used in computer science and are particularly useful in priority queues and sorting algorithms. Understanding how to implement a heap using an array will help you grasp the fundamentals of this data structure.
First, we need to initialize an array to store the heap elements. You can choose the size of the array based on your requirements. Let's initialize an array called heap with a size of 100.
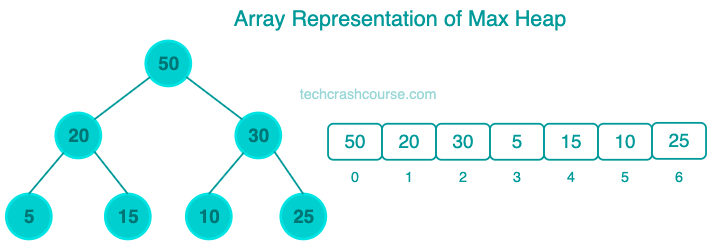
To determine the left child and right child indices of a heap node in the array implementation, you can use the following formulas:
- For a node at index currentIndex, its left child is at index (2 * currentIndex) + 1.
- For a node at index currentIndex, its right child is at index (2 * currentIndex) + 2.
The heapify function recursively "bubbles down" a node until it is in its correct position in the heap, and the insert function "bubbles up" a new node until it is in its correct position. The deleteRoot function replaces the root node with the last node in the heap and then calls heapify to restore the heap property. Finally, the printHeap function simply prints out the contents of the heap array.
#include <stdio.h>
#define MAX_HEAP_SIZE 100
int heap[MAX_HEAP_SIZE];
int size = 0;
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
void heapify(int i) {
int left_child = 2 * i + 1;
int right_child = 2 * i + 2;
int largest = i;
if (left_child < size && heap[left_child] > heap[largest]) {
largest = left_child;
}
if (right_child < size && heap[right_child] > heap[largest]) {
largest = right_child;
}
if (largest != i) {
swap(&heap[i], &heap[largest]);
heapify(largest);
}
}
void insert(int num) {
if (size == MAX_HEAP_SIZE) {
printf("Heap is full, cannot insert new element\n");
return;
}
heap[size] = num;
int current = size;
while (heap[current] > heap[(current - 1) / 2]) {
swap(&heap[current], &heap[(current - 1) / 2]);
current = (current - 1) / 2;
}
size++;
}
void deleteRoot() {
if (size == 0) {
printf("Heap is empty, cannot delete root\n");
return;
}
heap[0] = heap[size - 1];
size--;
heapify(0);
}
void printHeap() {
if (size == 0) {
printf("Heap is empty\n");
return;
}
for (int i = 0; i < size; i++) {
printf("%d ", heap[i]);
}
printf("\n");
}
int main() {
insert(5);
insert(3);
insert(7);
insert(1);
insert(9);
insert(4);
insert(8);
insert(2);
printf("Initial heap:\n");
printHeap();
deleteRoot();
printf("Heap after deleting root:\n");
printHeap();
insert(10);
printf("Heap after inserting element:\n");
printHeap();
return 0;
}
Output
Initial heap: 9 7 8 2 3 4 5 1 Heap after deleting root: 8 7 5 2 3 4 1 Heap after inserting element: 10 8 5 7 3 4 1 2
Best Practices of Using Heap Data Structures
- Choosing the Right Data Structure : While heaps are powerful for specific use cases like priority queues and heap sort, it's essential to choose the right data structure based on the specific requirements of the application. If quick retrieval of the highest or lowest priority element is crucial, a heap is a suitable choice. However, for scenarios requiring frequent search operations, other data structures like binary search trees might be more appropriate.
- Choose the Right Heap Type : Select the type of heap (max-heap or min-heap) based on the requirements of the application. Max-heaps are suitable for priority queues, while min-heaps are useful for applications like Dijkstra's algorithm.
- Efficient Heap Operations : Implement efficient heap operations to maintain the heap property during insertions and deletions. This ensures that the heap remains balanced and retains its efficiency.
- Memory Management : Be mindful of memory usage, especially in large heaps. Efficient memory management practices can enhance the performance of heap-based applications.
- Dynamic Resizing : Implement dynamic resizing strategies to accommodate varying numbers of elements. This prevents unnecessary memory consumption and enhances the flexibility of the heap.
- Understand Application Requirements : Clearly understand the requirements of the application, such as whether quick insertion or quick retrieval is more critical. This understanding will guide the choice of the appropriate heap type.
Conclusion
The heap data structure is a versatile and efficient tool with applications ranging from priority queues to sorting algorithms. By understanding its properties, types, operations, and best practices, developers can leverage the full potential of heaps in various programming scenarios. Whether implementing a priority queue for task scheduling, utilizing heap sort for efficient sorting, or applying heaps in graph algorithms, the heap proves to be a valuable asset in the realm of computer science and software development.
