The Divide and Conquer Algorithm is a problem-solving technique used in computer science and other fields. This algorithm works by dividing a problem into smaller subproblems, solving each subproblem independently, and then combining the results to solve the original problem. The main idea behind Divide and Conquer is to break down a problem into smaller parts that are easier to solve, and then combine the results to get the final solution.
How Divide and Conquer Algorithm Works
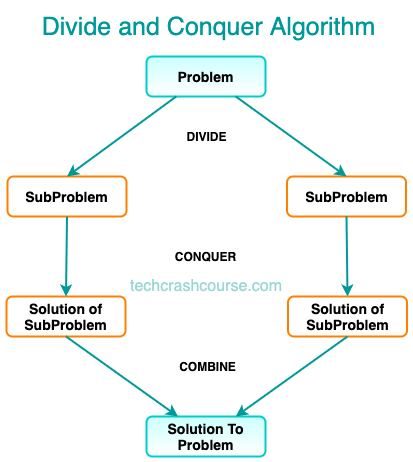
Divide and Conquer Algorithms work by breaking down a problem into smaller subproblems, each of which can be solved independently. After solving each subproblem, the results are combined to solve the original problem. This approach is typically used to solve problems that can be divided into smaller, more manageable parts. Divide and Conquer Algorithms are especially useful when the subproblems can be solved efficiently, and the solution to the original problem can be derived from the solutions to the subproblems.
- Divide: Divide the problem into smaller subproblems.
- Conquer: Solve each subproblem recursively.
- Combine: Combine the solutions of each subproblem to solve the original problem.
Let's take an example of finding the maximum element in an array to illustrate the Divide and Conquer Algorithm.
- Step 1: Divide the array into two halves.
- Step 2: Recursively find the maximum element in each half.
- Step 3: Combine the results by comparing the maximum element of the two halves to find the maximum element in the entire array.
Here's a sample C program to find the maximum element in an array using the Divide and Conquer Algorithm:
#include<stdio.h>
int find_max(int arr[], int low, int high){
if(low == high)
return arr[low];
else{
int mid = (low + high) / 2;
int left_max = find_max(arr, low, mid);
int right_max = find_max(arr, mid+1, high);
if(left_max > right_max)
return left_max;
else
return right_max;
}
}
int main(){
int arr[] = {10, 20, 30, 40, 50};
int n = sizeof(arr) / sizeof(arr[0]);
int max = find_max(arr, 0, n-1);
printf("Maximum element in the array is %d", max);
return 0;
}
Output
Maximum element in the array is 50
Time and Space Complexity of Divide and Conquer Algorithms
The time complexity of Divide and Conquer Algorithms is generally expressed in terms of the recurrence relation that describes the number of operations required to solve a problem of size n. The space complexity of Divide and Conquer Algorithms is the amount of memory required to solve a problem of size n.
Recurrence relation is a mathematical equation that describes the number of operations performed by a Divide and Conquer Algorithm to solve a problem of size n. It is an important tool for analyzing the time complexity of Divide and Conquer Algorithms.
The recurrence relation for Divide and Conquer Algorithms can be expressed in terms of the time required to solve a problem of size n, T(n), and the time required to solve the subproblems of size n/2, T(n/2). The recurrence relation is typically expressed as follows:
T(n) = aT(n/b) + f(n)where:
- a represents the number of subproblems created in the divide step.
- n/b represents the size of each subproblem.
- f(n)represents the time required to combine the solutions of the subproblems.
Advantages and Disadvantages of Divide and Conquer Algorithms
Advantages of Divide and Conquer Algorithms
- Efficient for solving problems that can be divided into smaller subproblems.
- Often parallelizable, since the subproblems can be solved independently.
- Can be used to solve a wide range of problems, including sorting, searching, and optimization problems.
Disadvantages of Divide and Conquer Algorithms
- The algorithm can be complex and difficult to implement for some problems.
- The algorithm may not be efficient for problems that cannot be divided into smaller subproblems.
- The overhead of dividing the problem into smaller subproblems may be significant, especially for small problems.
Overall, the Divide and Conquer Algorithm is a powerful problem-solving technique that can be used to solve a wide range of problems efficiently. By breaking down a problem into smaller subproblems and solving each subproblem independently, the algorithm can often achieve faster runtimes and better performance than other approaches.
Standard problems which can be solved using Divide and Conquer Algorithm
- Binary Search : Binary Search is a classic example of Divide and Conquer. It repeatedly divides the search space in half until the target element is found or the search space is empty.
- Strassen's Matrix Multiplication: Strassen's algorithm uses Divide and Conquer to multiply two matrices more efficiently by breaking them into smaller submatrices and recursively calculating products.
- Merge Sort: Divide and Conquer is employed by recursively dividing an array into two halves, sorting each half, and merging them back together to produce a sorted array.
- Quick Sort: Quick Sort uses Divide and Conquer by selecting a pivot element, partitioning the other elements into two subarrays, and then recursively sorting the subarrays.
- Fast Fourier Transform: FFT uses Divide and Conquer to efficiently compute the discrete Fourier transform of a sequence by recursively dividing it and combining the results.
- Karatsuba Algorithm: Karatsuba Algorithm employs Divide and Conquer to multiply large numbers efficiently by breaking them into smaller parts and recursively calculating products.
- Closest Pair of Points: This algorithm uses Divide and Conquer to find the closest pair of points in a set by recursively dividing the set and efficiently combining results.
- Closest String Pair: This algorithm finds the closest pair of strings in a set using Divide and Conquer by recursively dividing the set and efficiently combining results to identify the closest pair.
- Convex Hull: Algorithms like Graham's Scan find the convex hull of a set of points using Divide and Conquer to merge convex hulls of smaller subsets.
