Types of Graph Data Structure
Graphs are a fundamental data structure used in computer science to model relationships between objects. A graph consists of a set of vertices (also known as nodes) and a set of edges, which connect the vertices. Understanding the different types of graph data structures is crucial for effectively modeling and solving problems in various domains. In this tutorial, we'll explore three main types of graph data structures: undirected graphs, directed graphs, and weighted graphs.
Undirected Graph
An undirected graph is a fundamental data structure that models relationships between entities without considering the directionality of those relationships. In this type of graph, edges between nodes do not have an inherent direction, meaning the relationship between two nodes is symmetric. Undirected graphs serve as a versatile and intuitive representation for various real-world scenarios, allowing for a clear depiction of connections and dependencies.
An example of an undirected graph is shown below:

Directed Graph
The directed graph, or digraph, stands as a pivotal data structure within the realm of graph theory, offering a dynamic framework for modeling relationships with inherent directionality. Unlike its undirected counterpart, a directed graph acknowledges the asymmetry of connections, where edges have a distinct direction, signifying a one-way relationship between nodes. In this comprehensive summary, we explore the key attributes, applications, and operational aspects of directed graphs.
An example of a directed graph is shown below:

Weighted Graph
At its core, a weighted graph maintains the fundamental components of a graph - nodes (vertices) and edges. However, the edges in a weighted graph are augmented with a numerical value known as a weight. This weight encapsulates a measure of the cost, distance, time, or any other relevant metric associated with traversing the edge. Consequently, weighted graphs provide a richer and more realistic model, allowing for a precise representation of the quantitative aspects of relationships.
An example of a weighted graph is shown below:

Connected Graph
A a connected graph is characterized by the absence of isolated nodes or disjoint components. Every node within the graph is reachable from any other through a sequence of edges, forming an unbroken web of connections. This concept underscores the unity and interdependence inherent in connected graphs, making them a fundamental and cohesive data structure.
An example of a connected graph is shown below:

Spanning Tree
A spanning tree is a subgraph of a graph that contains all the vertices of the graph and is a tree. A tree is a connected graph with no cycles. A spanning tree of a graph is a way of connecting all the vertices of the graph without creating any cycles. An example of a spanning tree for the previous connected graph is shown below:
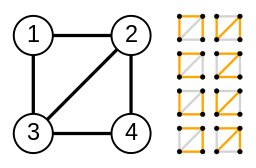
Minimum Spanning Tree
A minimum spanning tree is a spanning tree of a weighted graph that has the smallest possible total weight. In other words, it is a way of connecting all the vertices of a weighted graph with the smallest possible cost. There are several algorithms that can be used to find the minimum spanning tree of a graph, including Prim's algorithm and Kruskal's algorithm.
An example of a minimum spanning tree for the previous weighted graph is shown below:
Conclusion
As we conclude this exploration, it becomes evident that the choice of a graph data structure is not a one-size-fits-all decision but a deliberate selection based on the nature of relationships and the requirements of the problem at hand. The diversity of graph data structures mirrors the intricacies of real-world interconnected systems, providing a comprehensive toolkit for developers, engineers, and analysts to navigate and optimize the complex web of relationships in their respective domains. Whether simplifying connections in a social network or optimizing routes in a transportation system, the various types of graph data structures empower us to model, analyze, and ultimately make informed decisions in the intricate tapestry of interconnected data.
