Hash Table
A hash table is a data structure that is used to store and retrieve data quickly. It uses a technique called hashing to map keys to indexes in an array. The hash table consists of an array of fixed size, and each slot in the array can store a key-value pair.
The keys are used to compute an index into the array using a hash function. Once the index is computed, the value can be stored or retrieved from the corresponding slot.
Hash tables are widely used in computer science due to their fast insertion, deletion, and lookup operations. They are commonly used in applications where large amounts of data need to be stored and retrieved quickly, such as databases, caches, and compilers.

Hashing (Hash Function)
Hashing is the process of converting a key into an index that can be used to access the corresponding value in the hash table. The hash function takes a key as input and returns an index into the array. The hash function should be fast and should produce evenly distributed indices to avoid collisions.
The ideal hash function should produce a unique index for each key. However, this is not always possible, and collisions can occur when two or more keys map to the same index.
Hash Collision
A hash collision occurs when two or more keys are mapped to the same index in the array. Hash collisions are inevitable in hash tables due to the limited size of the array and the potentially infinite number of keys that can be inserted.
To handle collisions, various collision resolution techniques can be used, such as chaining, linear probing, and quadratic probing.

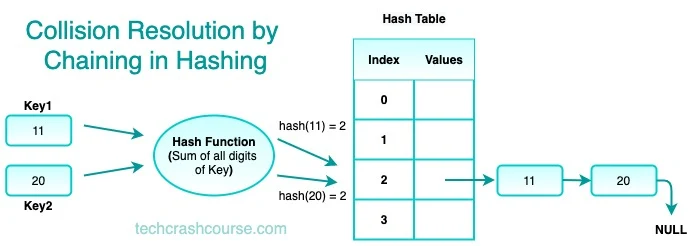
Collision Resolution by Chaining
Chaining is a collision resolution technique where each slot in the hash table contains a linked list of key-value pairs. When a collision occurs, the key-value pair is added to the linked list at the corresponding slot.
To retrieve a value, the hash function is used to compute the index of the key, and then the linked list at that index is searched for the key-value pair.
Chaining is simple to implement and works well when the load factor (the ratio of the number of elements to the size of the array) is low. However, as the load factor increases, the length of the linked lists also increases, leading to a decrease in performance.
Collision Resolution by Chaining
Open addressing is a technique employed to address collisions by finding an alternative slot within the same array for the colliding key. Unlike chaining, where collisions are resolved by maintaining linked lists at each index, open addressing seeks an available slot within the array itself.
In open addressing, when a collision occurs (i.e., two keys hash to the same index), the algorithm looks for the next available slot in the array to place the colliding key. The search for an alternative slot is done through a probing sequence, a sequence of indices that are examined one by one until an empty slot is found.
Key concepts of open addressing:
- Probing Sequence : The order in which indices are examined to find an empty slot.
- Primary Clustering : When consecutive slots are occupied due to collisions, leading to inefficient probing.
- Secondary Clustering : When multiple keys end up probing the same sequence, creating clusters of occupied slots.
Quadratic probing uses a probing sequence based on a quadratic function. If a collision occurs at index i, the algorithm probes slots based on the formula (i + c1 * k + c2 * k^2) % size, where k is the attempt number. Quadratic probing aims to mitigate primary clustering, but it can still suffer from secondary clustering.
Basic Hash Function Examples
- Division Function: The hash function computes the index as the remainder of the key divided by the size of the array. This method works well when the size of the array is a prime number and the keys are uniformly distributed.
- Multiplication Function: The hash function computes the index as the product of the key and a constant factor, then takes the fractional part of the result and multiplies it by the size of the array. This method works well when the constant factor is a fractional number between 0 and 1 and the keys are uniformly distributed.
- Universal Hashing Function: The hash function uses a family of hash functions, each of which is chosen randomly from a set of hash functions. This method works well when the keys are not uniformly distributed, as it reduces the likelihood of collisions.
Common Hash Table Operations and Their Time Complexities
- Insertion: O(1) on average, O(n) in the worst case (when all keys map to the same index)
- Deletion: O(1) on average, O(n) in the worst case (when all keys map to the same index)
- Lookup: O(1) on average, O(n) in the worst case (when all keys map to the same index)
- Search: O(1) on average, O(n) in the worst case (when all keys map to the same index)
- Traversal: O(n)
Hash Table Implementation Program
This program uses a simple hash function that computes the sum of the ASCII values of the characters in the key. It implements the insert, get, and remove operations, as well as a print_table function for debugging purposes.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAX_SIZE 100
typedef struct {
char* key;
int value;
} Pair;
typedef struct {
Pair* pairs[MAX_SIZE];
int size;
} HashTable;
int hash(char* key) {
int sum = 0;
for (int i = 0; i < strlen(key); i++) {
sum += key[i];
}
return sum % MAX_SIZE;
}
void insert(HashTable* table, char* key, int value) {
int index = hash(key);
Pair* pair = (Pair*) malloc(sizeof(Pair));
pair->key = key;
pair->value = value;
table->pairs[index] = pair;
table->size++;
}
int get(HashTable* table, char* key) {
int index = hash(key);
Pair* pair = table->pairs[index];
if (pair == NULL) {
return -1;
}
return pair->value;
}
void remove_key(HashTable* table, char* key) {
int index = hash(key);
Pair* pair = table->pairs[index];
if (pair != NULL) {
table->pairs[index] = NULL;
free(pair);
table->size--;
}
}
void print_table(HashTable* table) {
for (int i = 0; i < MAX_SIZE; i++) {
Pair* pair = table->pairs[i];
if (pair != NULL) {
printf("%s: %d\n", pair->key, pair->value);
}
}
}
int main() {
HashTable table = { .size = 0 };
insert(&table, "Alice", 25);
insert(&table, "Bob", 30);
insert(&table, "Charlie", 35);
insert(&table, "David", 40);
print_table(&table);
printf("Bob's age is %d\n", get(&table, "Bob"));
remove_key(&table, "Bob");
print_table(&table);
return 0;
}
Output
Bob: 30 Alice: 25 David: 40 Charlie: 35 Bob's age is 30 Alice: 25 David: 40 Charlie: 35
Advantages and Limitations of Hash Tables
- Efficient Operations : Hash tables provide constant-time average-case complexity for insertion, retrieval, and deletion operations.
- Dynamic Sizing : Hash tables can dynamically resize to adapt to the number of elements, ensuring efficient memory usage.
- Versatility : Hash tables are versatile and applicable in a wide range of applications, including databases, caches, and language interpreters.
- Worst-Case Complexity : In the worst-case scenario, hash table operations can have a time complexity of O(n), where n is the number of elements.
- Memory Overhead : Chaining, the most common collision resolution strategy, introduces additional memory overhead due to linked lists.
Best Practices of Using Hash Tables
- Use a Strong Hash Function : Invest time in designing or selecting a strong hash function. A good hash function minimizes the chance of collisions and ensures a uniform distribution of keys across the array.
- Choose an Appropriate Load Factor : The load factor is the ratio of the number of stored elements to the size of the array. A balanced load factor ensures efficient use of memory and minimizes the likelihood of collisions. Common load factors range from 0.7 to 0.9.
- Consider Dynamic Resizing : Implement dynamic resizing to adjust the size of the array based on the number of elements stored. This prevents the hash table from becoming either too sparse or too crowded.
- Handle Collisions Effectively : Choose a collision resolution strategy that aligns with the requirements of your application. Evaluate the trade-offs between simplicity and memory efficiency when selecting between chaining and open addressing.
- Understand Key Characteristics : Understand the characteristics of the keys you are working with. For example, if keys are integers with a limited range, a simple hash function might suffice. However, for more complex keys, a more sophisticated hash function may be necessary.
Conclusion
The hash table data structure is a fundamental tool in computer science, providing efficient key-value storage and retrieval. By understanding its principles, basic operations, collision resolution strategies, and best practices, developers can harness the full potential of hash tables in various applications. Whether implementing a database, optimizing cache performance, or building a language interpreter, the hash table proves to be a versatile and indispensable asset in the realm of data structures.
