In this java program, we will learn about how to add two matrices using multi-dimensional arrays and to display the sum matrix.
To understand this java program, you should have understanding of the following Java programming concepts:
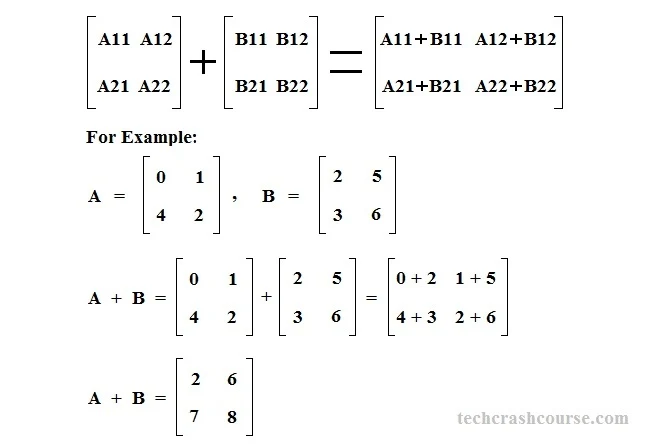
- Matrix addition is defined for two matrices of the same dimensions, If the size of matrices are not same, then the sum of these two matrices is said to be undefined.
- The sum of two M × N matrices A and B, denoted by A + B, is again a M × N matrix computed by adding corresponding elements.
Algorithm for addition of two matrices
Let A and B are two matrices of dimension M X N and S is the sum matrix(S = A + B). Below mwntionws steps explains how we can find fum of two matrices.
Let A and B are two matrices of dimension M X N and S is the sum matrix(S = A + B). Below mwntionws steps explains how we can find fum of two matrices.
- To add two matrices we have to add their corresponding elements. For example, S[i][j] = A[i][j] + B[i][j].
- Traverse both matrices row wise(first all elements of a row, then jump to next row) using two loops(check line number 30 and 31 of below program).
- For every element A[i][j], add it with corresponding element B[i][j] and store the result in Sum matrix at S[i][j].
Java Program to Add Two Matrices using Multi-Dimensional Arrays
public class MatrixAddition {
public static void main(String[] args) {
int rows = 2, columns = 4;
// Declaring the two matrices of 2X4 size to add
int[][] matrixOne = { {1, 2, 3, 4}, {5, 6, 7, 8} };
int[][] matrixTwo = { {0, 1, 0, 1}, {0, 1, 0, 1} };
int[][] sumMatrix = new int[rows][columns];
/*
Add corresponding elements of both matrices and
store it in sumMatrix.
*/
for(int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
sumMatrix[i][j] = matrixOne[i][j] + matrixTwo[i][j];
}
}
// Print the sum matrix
System.out.println("Sum of two matrices is: ");
for(int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
System.out.print(sumMatrix[i][j] + " ");
}
System.out.println();
}
}
}
Output
Sum of two matrices is: 1 3 3 5 5 7 7 9
